XGBoost, Understanding Tuning

Nish · June 17, 2023

Tips   XGBoost   GBT   Machine Learning   Hyperparameter Tuning

Useful Resources

Lots of material exists when it comes to XGBoost and parameter tuning. Here are some ones I have come across:

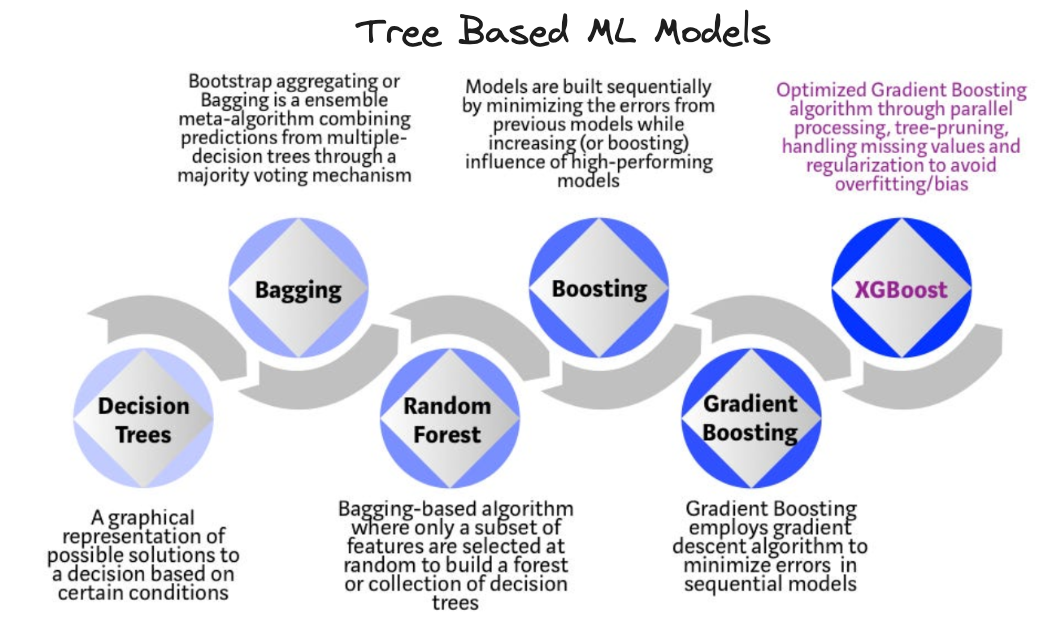
What is XGBoost?

XGBoost, or eXtreme Gradient Boosting, can be thought of as a special implementation of gradient boosted trees algortithm by Tianqi & Carlos in their 2016 paper which is open source and widely considered one of the best ML algorithmns in the context of structured tabular data (in terms of performance, efficiency etc) even today.

Summary view of various tree based algorithmns how they relate, referenced from this towards datascience article
Summary view of various tree based algorithmns how they relate, referenced from towards datascience article.

Ok…so what are hyperparameters?

When applying algorithms to your data it’s often the case that they come with “levers” that you can fiddle with to alter the effectiveness of the algorithm to your specfic problem. Formally speaking these levers are referred too as hyperparameters of your model and can have different optimal values depending on your data.

Note: These levers are separate to the inherent learned information of the model when you call the .fit() method on your model object (assuming scikit-learn based model APIs). These “levers” are not determined via the model learning process itself but rather trial and error and passed in as arguments to your model objects constructor during the instantiating process (something like XGBoostClassifier(**params) where params is a dictionary object with keys corresponding to the hyperparameter name and values being the numeric values they should take on)

In the case of XGBoost many hyperparameters exist so it’s important to know what they are & ways to classify them. A good way to do this is by grouping them by “what they impact” in which case the following groupings apply:

Note: The list provided below is not exhaustive, more details can be found on XGBoost parameters docs however a general observation is that when parameters contain the max_ prefix increasing them causes a rise in complexity while reducing them causes an increase in simplicity. Parameters with min_ prefix have the opposite effect whereby increasing them tends to simplify things and vice versa.

  1. Tree creation
    • Ultimately XGBoost consists of trees so these params control the properties of those underlying trees.
    • Parameters:
      • max_depth=6: Tree depth, how many feature interactions can you have. Larger is more complex (potential overfitting). Each level doubles each time (imagine number of splits ie $2^{n}$ ). It can take a range of values $n \in [0, \infty]$.
      • max_leaves=0: Number of leaves in tree. A larger number is increases complexity. It can take a range of values $n \in [0, \infty]$.
      • min_child_weight=1: Minimum sum of hessian (weight) needed in a child. The larger value is more conservative. It can take a range of values $n \in [0, \infty]$. This blog post contains more info.
      • grow_policy= 'depthwise': Only supported with tree_method set to ['hist', 'approx', 'gpu_hist']. Split nodes closest to root. Set to 'lossguide' (with max_depth'=0) to mimic LightGBM behavior.
      • tree_method='auto': Use 'hist' to use histogram bucketing and increase performance. ‘auto’ can act as an heuristic.
        • 'exact' for small data
        • 'approx' for larger data
        • 'hist' for histograms (limit bins with max_bins (default 256))
  2. Sampling
    • Effect the sampling procedure at various levels within the model, since subset of columns are taken as part of the underlying model architecture. They tend to have compounding depedences e.g If colsample_bytree= colsample_bylevel= colsample_bynode= 0.5 then the trees would have $(0.5)^{3} = 0.125 = 12.5%$ of the intial columns.
    • Parameters:
      • colsample_bytree: Fraction of columns to be sampled for a tree (as a decimal). It can take a range of values $n \in (0, 1]$ however searching recommendation is $[0.5, 1]$.
      • colsample_bylevel: Fraction of columns to be sampled for a level inside tree (as a decimal). It can take a range of values $n \in (0, 1]$ however searching recommendation is $[0.5, 1]$
      • colsample_bynode: Fraction of columns to be sampled at each node split (as a decimal). It can take a range of values $n \in (0, 1]$ however searching recommendation is $[0.5, 1]$.
      • subsample: Proportion of training data rows sampled prior to each successive boosting round. Lower is more conservative and reduces computation. It can take a range of values $n \in (0, 1]$ however searching recommendation is $[0.5, 1]$. If $n < 1$ then I think stochastic gradient descent is used, meaning a fair amount of randomness during the optimization.
      • sampling_method: Type of sampling you want to use. 'uniform' is implies equal probability acoss each column.
  3. Categorical data
    • XGBoost constructor has to have argument enable_categorical=True set and the pandas DataFrame columns have to have astype('category') where applicable for this to work.
    • Parameters:
      • max_cat_to_onehot=4: Upper threshold for using one-hot encoding for categorical features. One-hot encoding is used on categorical features when the number of categories present is less than this number.
      • max_cat_threshold=64: Maximum number of categories to be considered for each split. Rough heuristic suggests $64$ for this.
  4. Ensembling
    • These parameters control how the subsequent trees are created and “ensembled”
    • Parameters:
      • n_estimators=100: Number of trees. A larger value will increase complexity. Use early_stopping_rounds to prevent overfitting. You don’t really need to tune this if you early_stopping_rounds.
      • early_stopping_rounds=None: Number of rounds after which you stop creating new trees if eval_metric score hasn’t improved. It can take a range of values $n \in [1, \infty]$.
      • eval_metric: Choosen metric for evaluating validation data for evaluating early stopping criteria. Classification metrics include ['logloss', 'auc'] where as regression include things like ['mae', 'rmse', 'rmsle', 'mape'].
      • objective: Learning objective while fitting your model to the data during training process. For classification this is either 'binary:logistic or 'multi:softmax depending on whether it’s a binary or multi-class problem.
  5. Regularization
    • Controls complexity of the overall model. The following article
    • Parameters:
      • learining_rate=0.3: After each boosting round you multiply weights to make it more conservative (amount you want to move the weights after each round). A lower value represents a more conservative impact. It can take a range of values $n \in (0, 1]$ and you typically lower this if you want to increase n_estimators.
      • gamma=0/ min_split_loss: Effectively L0 Regularization. Minimum loss reduction required to split a leaf node. Effectively prunes tree to remove splits that don’t meet the given value. A larger value is more conservative and it can take a range of values $n \in [0, \infty)$ where $n=0$ represents no regularization. Recommended search is $(0, 1, 10, 100, 1000)$
      • reg_alpha=0: Effectively L1 Regularization. Mean of weights term added to loss e.g $\alpha \sum_{i=1}^{n} \lvert \beta_{i} \rvert$ where $\beta_{i}$ are the weights. Increase this to be more conservative. It can take a range of values $n \in [0, \infty)$.
      • reg_lambda=0: Effectively L2 Regularization. Root of squared weights term to loss e.g $\lambda \sqrt{\sum_{i=1}^{n} \beta_{i}^{2}}$ where $\beta_{i}$ are the weights. Increase this to be more conservative. It can take a range of values $n \in [0, \infty)$.
  6. Imbalanced data
    • Useful when your data distribution is imbalanced.
    • Parameters:
      • scale_pos_weight=1: Consider the proportion $\frac{\text{count negative}}{\text{count positive}}$ for imbalanced classes. It can take a range of values $n \in (0, \text{large number})$.
      • max_delta_step=0: Maximum delta step for leaf output. Potentially can help for imbalanced classes. It can take a range of values $n \in [0, \infty)$.

You can then view the hyperparameters for your model by doing something like

import xgboost as xgb

# Create a dictionary of hyperparameters
params = {'objective': 'binary:logistics',
         'random_state': 42,
         'reg_alpha': 0,
         'reg_lambda': 0,
         'learning_rate': 0.1,
         ...
         }
xgb_classifier = xgb.XGBClassifier(**params)
xgb_classifier.fit(X_train, y_train)

xgb_classifier.get_params()  # This method returns all parameters for you model object

How does tuning fit into this picture?

The whole concept then of “hyperparameter tuning” is the process of trying to find the optimal values that the hyperparameters should take for your given problem.

There is no hard and fast rule for this and typical approaches tend to boil down to using techniques (some more complex than others e.g GridSearch vs BayesianOptimization) to try a bunch of values & measure how the performance of your model changes as you vary those values, resulting finally in a set of values which provides the highest performance on your given data.

Example: Single parameter tuning

Note: In practice this isn’t something you’d tend to do but interesting for demonstration purposes.

The key here is to use validation curves to plot your performance metric against your single hyperparameter and choose the hyperparameter value which yields the optimal performance. By keeping all other things constant you can attribute changes in performance as relating to that single hyperparameter.

In code this would look something like:

from yellowbrick import model_selection as ms
import matplotlib.pyplot as plt
import xgboost as xgb

fig, ax = plt.subplots(figsize=(8,4))
ms.validation_curve.ValidationCurve(xgb.XGBClassifier(), 
                    X_train, 
                    y_train, 
                    param_name='gamma', 
                    param_range=[0, 0.5, 1, 5, 10, 20, 30],
                    cv=5,
                    ax=ax)

Where we have made use of the yellowbrick libraries validation curve functionality to plot and specified the necessary arguements including our estimator along with our dataset and the number of kfolds we want performed on our data to calculate our metric. For further details on cross-validation techniques checkout scikit-learns docs.

Example: Using GridSearchCV for tuning

Calibrating individual hyperparameters takes some time and it can be difficult to know which combination is best. A potential solution to this is to select a group of hyperparameters that you want to tune and specify a range for them which can be searched. You can make use of the Scikit-Learn GridSearch for this.

import xgboost as xgb
from sklearn import model_selection

N_CV_ROUNDS = 5
N_EARLY_STOPPING = 5

params = {
    'max_depth': [1, 5],
    'learning_rate': [0.1, 1],
    'n_estimators': 100,
    ...
}

xgb_model = xgb.XGBClassifier(early_stopping_rounds=N_EARLY_STOPPING)
gridsearch_cv = (
    model_selection.GridSearchCV(xgb_model, params, cv=N_CV_ROUNDS)
    .fit(X_train, y_train, eval_set=[(X_test, y_test)])
)
# Reading the best parameters values for our model
best_params = gridsearch_cv.best_params_

xgb_grid_model = xgb.XGBClassifier(**best_params)
xgb_grid_model.fit(X_train, y_train, eval_set=[(X_train, y_train), (X_test, y_test)], verbose=10)

The best parameters can then be fed into the model again when instantiating it.

Example: Using Hyperopt for tuning

Hyperopt is an python optimization library which uses BayesianOptimization under the hood which uses a probabilistic model to select the next set of hyperparameters to try. If one value performs better, it will try values around it amd see of hey boost the performance. If the values worsen the model then Hyperopt can ignore those values as future candidates.

Hyperopt works not only with the XGBoost model but others like RandomForests, Neural Networks etc.

Citation Information

If you find this content useful & plan on using it, please consider citing it using the following format:

@misc{nish-blog,
  title = {XGBoost, Understanding Tuning},
  author = {Nish},
  howpublished = {\url{https://www.nishbhana.com/XGBoost-Tuning/}},
  note = {[Online; accessed]},
  year = {2023}
}

x.com, Facebook