Recommender Sytems - Learning To Rank

Nish · July 24, 2023

ML   RecSys   LTR

Table of Contents

Intro

Modern day Recommendation Sytems can involve multiple componenents as depicted below all of which are neccessary in order to make a final recommendation.

Simplified view of making a recommendation. General takeaway is you start of with lots of items and those are reduced until you are left with your final recommendations.
Simplified view of making a recommendation. General takeaway is you start of with lots of items and those are reduced until you are left with your final recommendations.

In essence this can be broken down into 3 parts

  1. Retreival Component
    • Selecting the top k items to feed into the ranking model.
  2. Ranking Component
    • Ranking is a ubiquitous task that appears in many systems not just recommendations systems. These include systems involving Search, Question & Answer etc.
    • More generally ranking is the act of ordering a specific set of items for a specific context.
    • Learning to rank specifically refers to learning the function $f$ which generates scores for items given a certain context and does so in a way that resulting ranking based on those scores is optimal.
  3. Post-ranking Component
    • Filtering down the ranked list based on other factors that might be important (fairness, recent trends etc).

The focus of this article is ranking component.

How does LTR work at a high level?

As mentioned in the intro you are essesntially learning a function $f$. This learning can be broken down roughly as follows.

  1. Create and feed in your dataset.
    • Typically a dataset can take the form of a tuple of vectors. Essentially each element in the dataset is a list of items which you want to rank alongside a label which acts as a relevance proxy.
    • Mathematically something like $\mathcal{D} = (\textbf{x}, \textbf{y}) \in \chi^{n} \times \mathbb{R}^{n}$
  2. Create your model which outputs scores.
    • This would typically be some neural network based model which would take in the above dataset in batches and then output scores for each of the model.
    • The way in which the model output scores can be different and typically falls into 3 buckets.
      • Pointwise methods
        • Considers whether items are independently relevant outputs a score for each item (regression/classification).
      • Pairwise methods
        • Doesn’t care about whether items are independently relevant or not but instead relative preferences between pairs of items.
        • Can think of it interms of the question “Can I correctly predict relevancy between pairs?”
      • Listwise methods
        • State of the art methods which consider the entire list and what the ordering between all items is.
        • Associated loss functions are more complex.
  3. Adjust your model using a loss function.
    • The loss can act in the standard way as follows $\mathcal{L}(f) = \frac{1}{ \lvert D \rvert} \sum_{(\textbf{x}, \textbf{y}) \in \mathcal{D}} \mathcal{l}(f(\textbf{x}), \textbf{y})$ where you can optimize it as standard using gradient descent.
      • Main difference is it acts on a vector rather than a single item.
    • Specific types of losses for the ranking use case can be found on the TensorFlow Ranking loss docs.

What tools can be used to implement these?

A library known as TensorFlow Ranking exists which can help out with a bunch of these tasks. This library has been tested and is advocated by Google developer advocates for use when designing production grade systems.

In particular it includes things like ranking tailored losses, ranking metrics, data loaders, network layers, models etc which make it alot easier to build models.

Applying Learning to Rank in Practice

In this section, we will walk through applying learning to rank to the problem of ranking actions (digital objects) as part of a NBA system for users on a website to maximize engagement while trying to balance performance with time to market. We will cover the following steps: learning to rank approaches, model selection, data preparation, model training, model evaluation, and model serving.

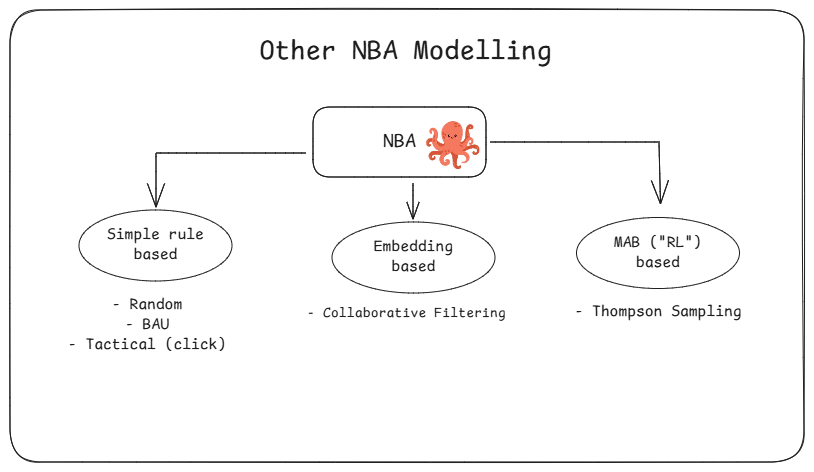
Other Approaches and Challenges

There are a number of other ways to approach these challenges but each typically has some shortcomings.

  • Simple Rule-Based: Good for baseline but not personalized and typically relatively worse in terms of performance.
  • Embedding-Based: Potentially suffer from cold start issues either due to new users & actions. Limited personalization due to data requirements (e.g., just past interaction).
  • Multi-Armed Bandit: Complex and requires more technical resources. Not inherently ranking optimized.
Showing some of the other potential approaches that can be taken to address the action ranking.
Showing some of the other potential approaches that can be taken to address the action ranking.

Learning to Rank Approaches & Model Selection

There are three main approaches to learning to rank: pointwise, pairwise, and listwise. Each approach has its own advantages and disadvantages, and the choice of approach depends on the specific problem and dataset.

Advantages of Learning to Rank

  • Captures complex relationships between user & actions.
  • Directly optimizes for engagement (CTR, conversions).
  • Adapts to new users and actions over time.
  • Efficient, scalable, and not overly complex.
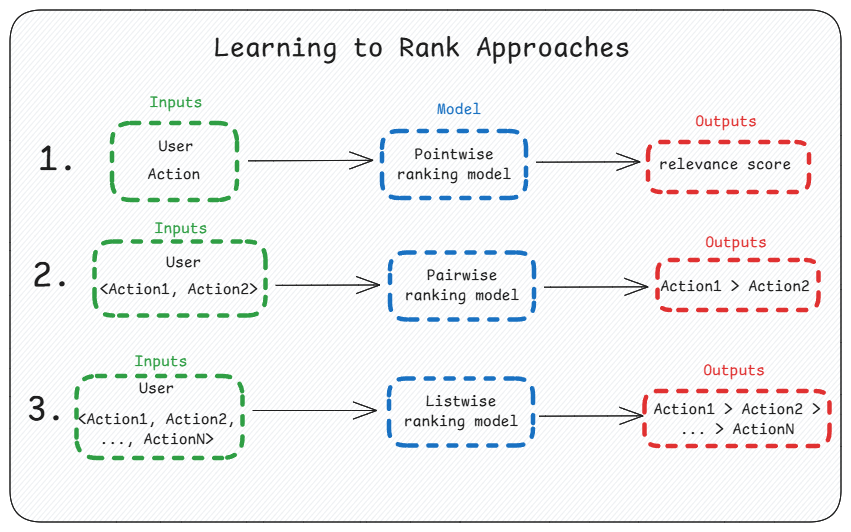
Showcasing the common approaches of learning to rank.
Showcasing the common approaches of learning to rank.

Choosing the right model is crucial for the success of a learning to rank system. Model choice depends on the LTR approach, which itself depends on several factors such as technical capabilities, timelines, and costs. Broadly speaking, from a performance perspective, Listwise > Pairwise > Pointwise, but the order also reflects complexity.

Given the goal at hand, it’d be best for us to go with a pairwise approach, enabling us to optimize for engagement while driving value quickly.

Picking the right model (& implementation) involves experimentation and finding what works best for the given problem.

Some popular models for learning to rank include:

  • Neural Networks: Flexible and powerful models that can capture complex patterns in the data.
  • Gradient Boosted Decision Trees (GBDT): Effective for many ranking problems and often used in practice. LGBMRanker would be a good starting candidate.
  • Support Vector Machines (SVM): Can be used for ranking with appropriate modifications.
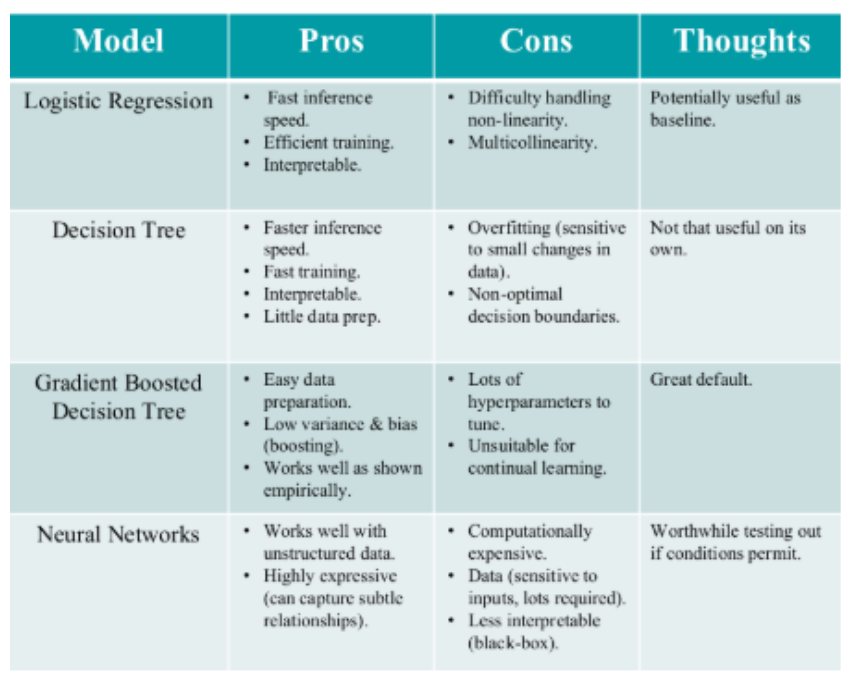
Suite of common ML algorithms used as a basis for LTR approaches.
Suite of common ML algorithms used as a basis for LTR approaches.

We’ll focus on LGBMRanker given the above.

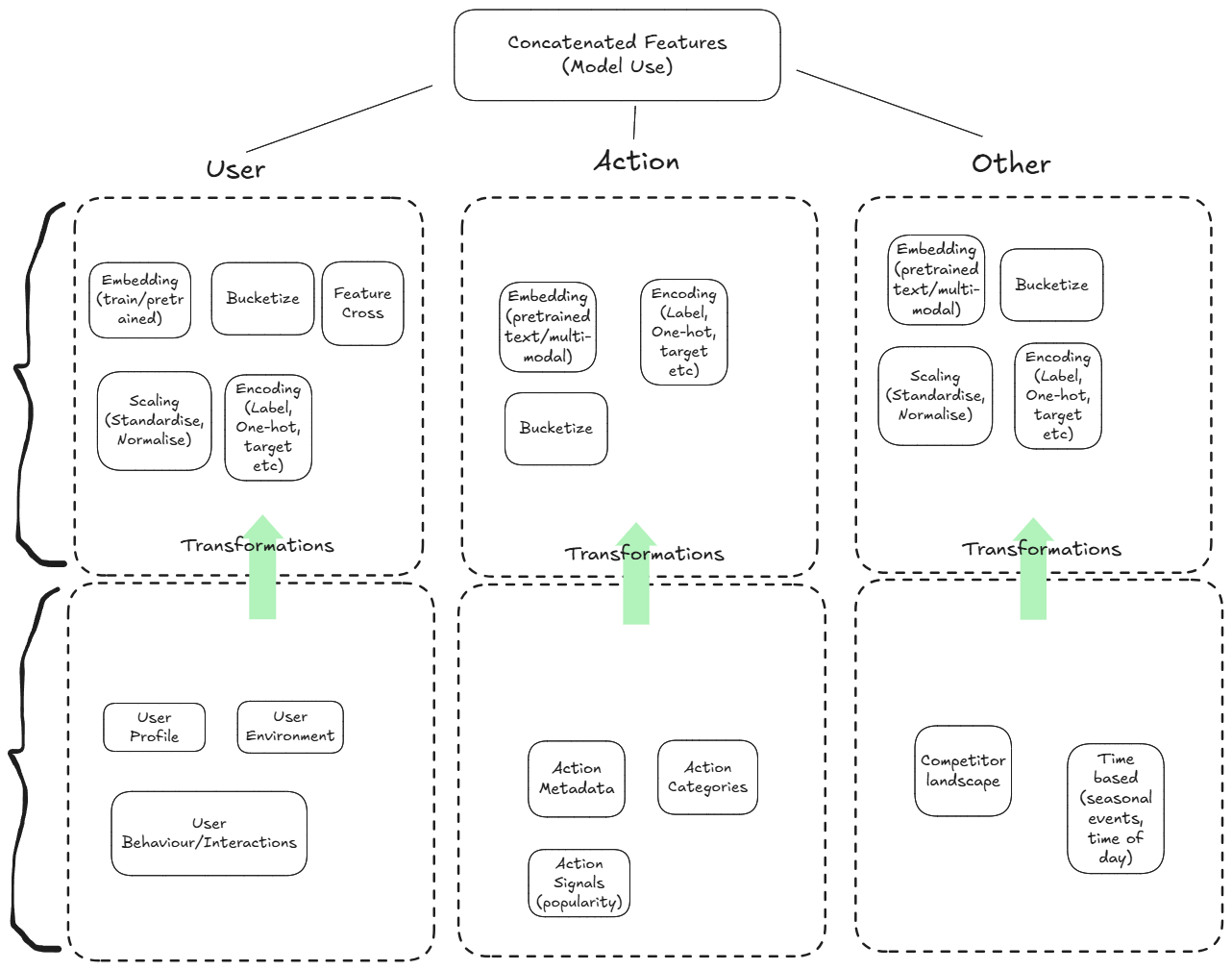
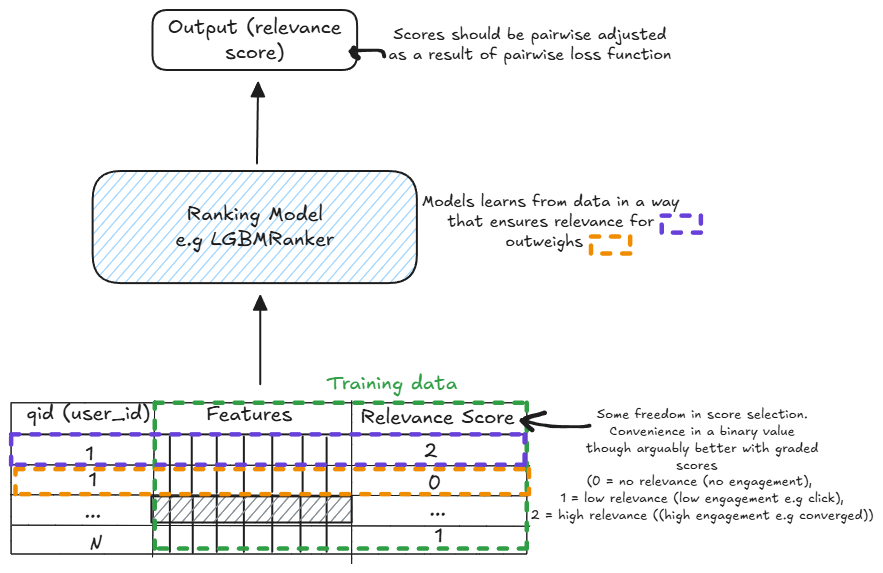
Data Preparation & Model Training

Preparing the data is a critical step in the learning to rank process. The data should be in the form of tuples of vectors, where each element in the dataset is a list of user-actions to be ranked alongside a label that acts as a relevance proxy.

  1. Collect Data: Gather data on user, actions, and interactions on the website.
  2. Feature Engineering: Create features that capture the characteristics of the digital objects and user interactions.
  3. Labeling: Assign relevance labels to the digital objects based on user engagement metrics you care about (e.g., clicks, time spent, conversions).
Standard data types and transformations that'd be worth considering.
Standard data types and transformations that'd be worth considering.

Training the model involves feeding the prepared dataset into the chosen model and optimizing it using a suitable loss function.The training workflow is very similar to more standard supervised learning techniques making it easy to work with for ml teams.

  1. Format the Data: The data needs to be in the right state to be fed into the model.
  2. Define the Model: Choose the hyperparameters, loss function etc that is appropriate for the ranking task. For example, pairwise loss functions can be used for pairwise methods.
  3. Train the Model: Use gradient descent or other optimization techniques to minimize the loss function and train the model on the dataset.
High level training approach for LGBMRanker.
High level training approach for LGBMRanker.

Model Evaluation

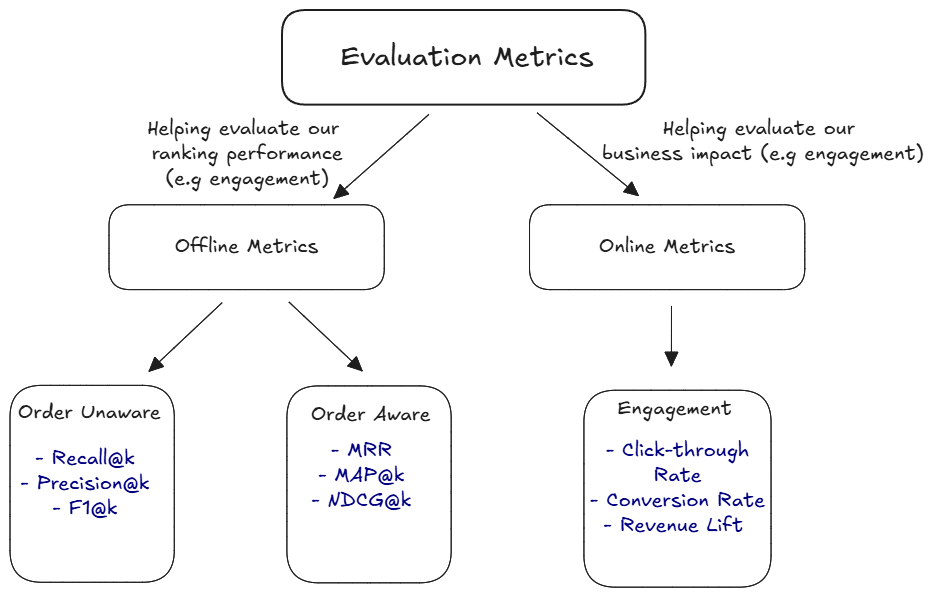
Evaluating the model is essential to ensure that it performs well on the ranking task. Evaluation typically happens in two stages: an offline setting (pre-deployment) and an online setting (post-deployment).

In our case, for offline evaluation, Normalized Discounted Cumulative Gain (NDCG@k) would likely be preferred since it’s order-aware and works with graded relevance. Mean Reciprocal Rank (MRR) focuses only on the rank of the first relevant actions, while Mean Average Precision (MAP@k) works only with binary relevance.

For online evaluation, it is best to treat the model as a challenger to existing models. Deploy it as a separate limb and track engagement KPIs such as Click-Through Rate (CTR).

Common evaluation metrics for learning to rank include:

  • Mean Reciprocal Rank (MRR): Measures the rank of the first relevant item.
  • Normalized Discounted Cumulative Gain (NDCG): Measures the quality of the ranking based on the positions of relevant items.
  • Precision@k: Measures the proportion of relevant items in the top-k positions.

In practice, it might also be worth considering “non-direct” metrics that track aspects like diversity of rankings and personalization. These metrics can be more relatable and important to stakeholders beyond just the pure objective metrics. For example, ensuring a diverse set of recommendations can improve user satisfaction and engagement, while personalization metrics can help track how well the model adapts to individual user preferences.

Evaluation metrics categorisation.
Evaluation metrics categorisation.

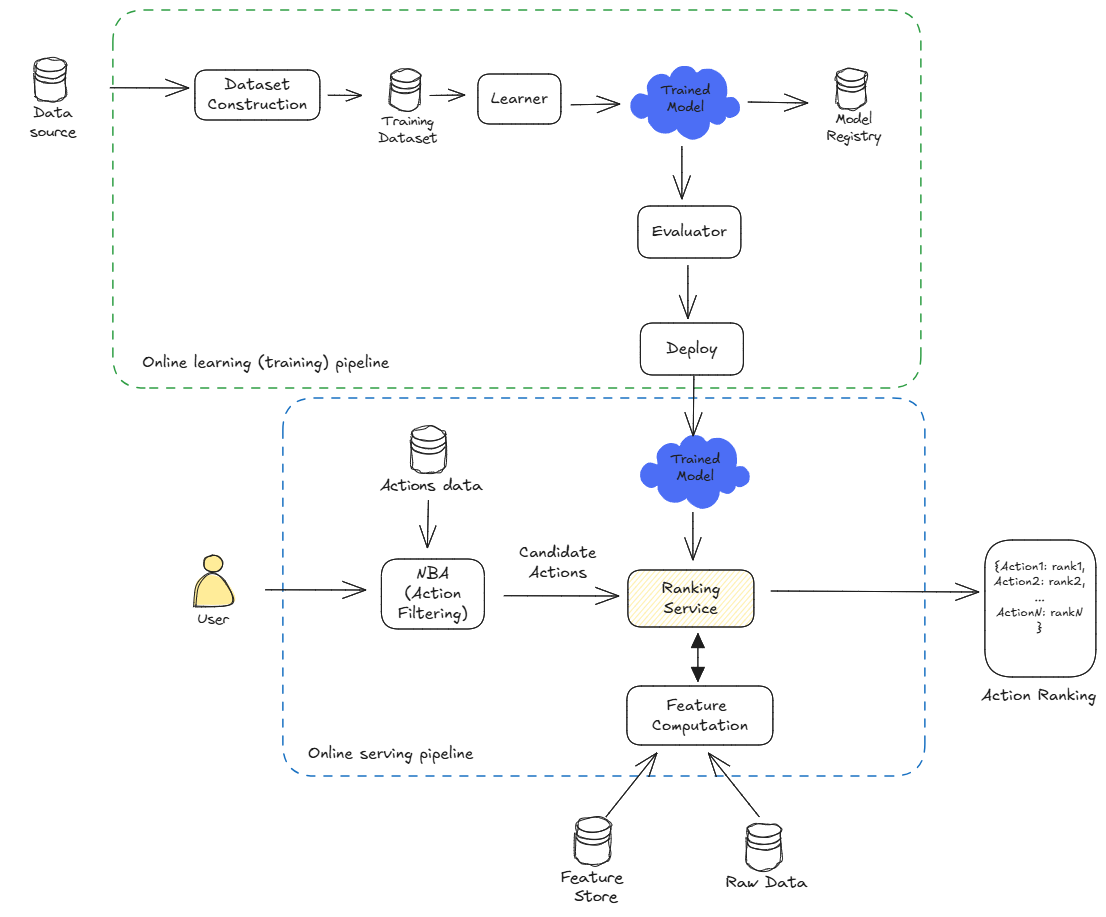
Model Serving

Once the model is trained and evaluated, it can be deployed to serve rankings in a production environment. Given the need for real-time inference, we can deploy the model to a platform using existing GCP ML Infrastructure. The feature store maintains the latest user information and can be used for fast retrieval of features during inference.

Key considerations for model serving include:

  1. Deploy the Model: Use a model serving framework (e.g., TensorFlow Serving) to deploy the trained model. Ensure that the deployment leverages GCP ML Infrastructure for scalability and reliability.
  2. Integrate with the Website: Integrate the model with the website to provide ranked lists of digital objects to users. Optimize feature selection to maintain real-time performance.
  3. Monitor Performance: Continuously monitor the performance of the model in production and update it as needed based on new data and user feedback. Utilize refined modeling techniques to reduce inference computational overhead.
  4. Enable Auto Scaling: Configure the infrastructure to auto-scale to handle peak loads of up to 100k users per day, ensuring consistent performance and availability.

By following these steps and considerations, you can apply learning to rank to the problem of ranking actions on a website to maximize user engagement while maintaining time to market.

Architectural diagram showcasing training, serving and how they link.
Architectural diagram showcasing training, serving and how they link.

Resources

  1. Libraries
    • TensorFlow Recommenders provides a great end-end production grade library for developing recommendation based applications (various useful components). Main advantage is that it’s been battle tested and is used as part of Googles: YouTube & Google Play services.
    • TensorFlow Ranking provides useful functionality specifically for the ranking tasks.
  2. Articles

Citation Information

If you find this content useful & plan on using it, please consider citing it using the following format:

@misc{nish-blog,
  title = {Recommender Sytems - Learning To Rank},
  author = {Nish},
  howpublished = {\url{https://www.nishbhana.com/Learning-To-Rank/}},
  note = {[Online; accessed]},
  year = {2023}
}

x.com, Facebook