Introduction
For any business having techniques that enable the ability to accurately estimate the value of a customer during their lifetime is an absolutely vital piece of business insight that informs an extensive number of critical business decisions.
It is typically a two part problem:
- Predict the length of the lifetime of each customer.
- Predict the revenue generated during their lifetime.
The first part is usually addressed with survival modelling and the second part is dependent on your businesses pricing model.
Methodology: Assumptions and considerations
Theory
In this post we’ll focus on the Kaplan Meier function and how it can be used to address the task of survival modelling but it’s worthwhile noting that a suite of technologies exist which are worth exploring.
\[[S(t) = \prod_{i:t_i \leq t} (1 - \frac{d_i}{n_i})]\]This represents the Kaplan-Meier estimator for the survival function $S(t)$, where the product is taken over all time points $t_{\text{i}}$ less than or equal to $\text{t}$, and $d_\text{i}$ and $n_\text{i}$ represent the number of events and survivors at each time point, respectively.
Assumptions
This esimtation has some assumptions/considerations.
- Unambigous events: The event (customer death) of interest happens at a clearly specified time.
- Survival probabilities are comparable in all subjects: Individuals’ survival chances do not depend on when they entered the sample under study.
- Censorship is non-informative: Observations that have yet to die have the same survival prospects as those that have died.
- Step-function: The Kaplan-Meier model acts as a step function, meaning that out-of-sample prediction is not possible.
Input Data
The general idea would be to fit this function to an existing historic dataset to gauge the cumulative probability of survival after N time intervals (e.g months).
To build the input data we want to average the survival prospects of cohorts of customers. We can do this by grouping customers on their tenure at latest observation we have for them on the base given their acquisition data.
Tip: In order to provide a more accurate estimate for survival, the cohorts can be further grouped (stratified) based on X number of features that you feel might influence things (e.g product type, group etc). For every combination of these stratified variables a KM survival function can be calculated and saved. Upon scoring these same features can be matched and used for survival analysis.
Visually this looks something like the following:
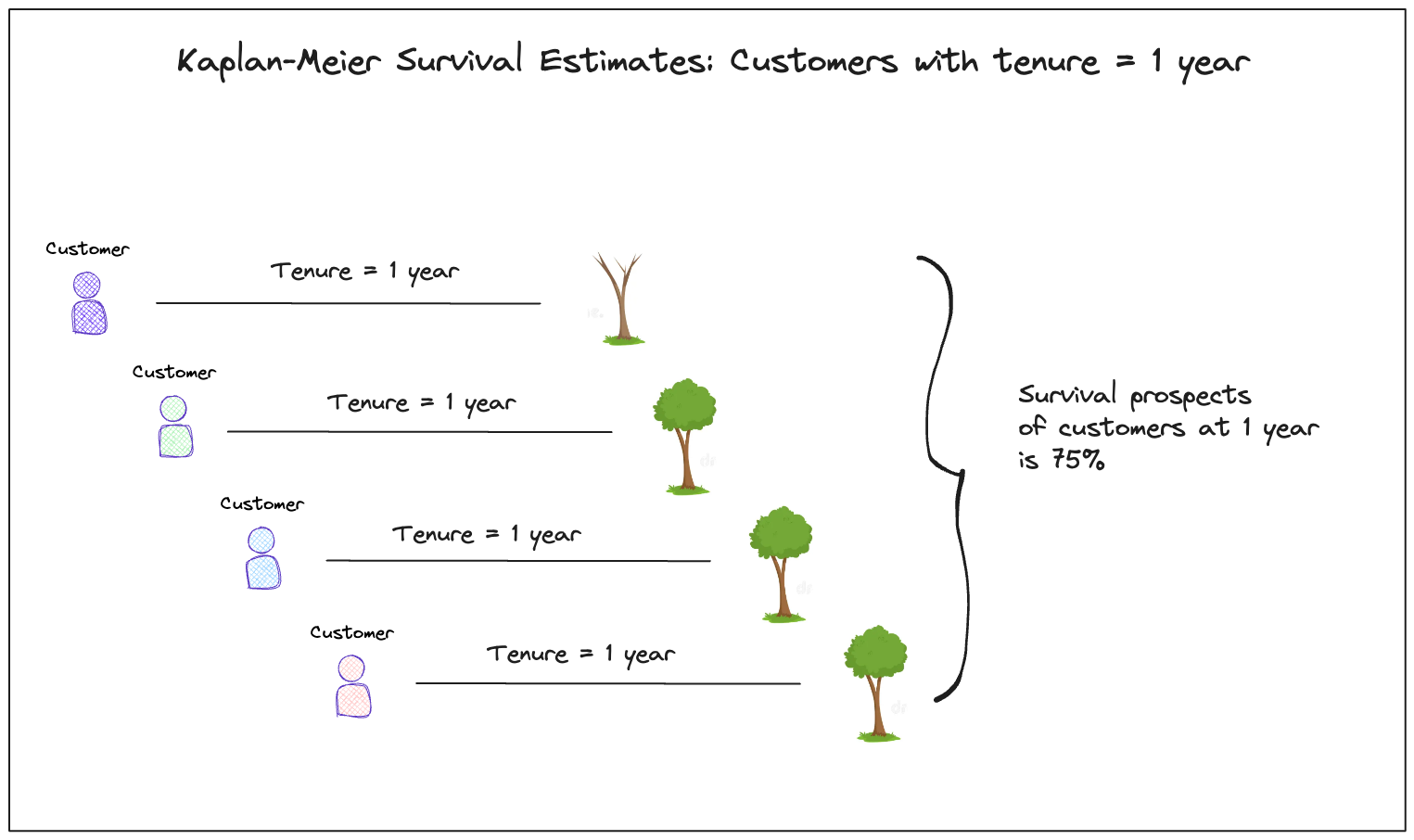
As a result you’d need input data like below where the colored fields are required to fit the function.
| snapshot_date | id | product | Service_acquisition_date | months_elapsed | dead |
|---|---|---|---|---|---|
| 2024-05-28 | 1234 | Mobile | 2017-01-12 | 88 | 0 |
| 2024-05-28 | 2345 | Mobile | 2021-12-09 | 29 | 0 |
| 2024-05-28 | 3456 | Mobile | 2021-12-12 | 29 | 0 |
| 2024-05-28 | 4567 | Mobile | 2021-12-12 | 29 | 0 |
| 2023-12-13 | 5678 | Mobile | 2021-12-13 | 24 | 1 |
Now when you build this dataset the main consideration you should be aware of is suvivorship bias within your cohorts. This can occur, where you introduce customers into your dataset that were acquired earlier than your earliest snapshot data.
The result of this can mean that some of your observations are not present in your dataset, because they churned before your earliest snapshot date, causing your cohort to be biased towards customers that have lived longer.
The easiest way to fix this is by making sure that no customers who have an acquisition date earlier than your earliest snapshot date are introduced into your sample.
Fitted KM Function
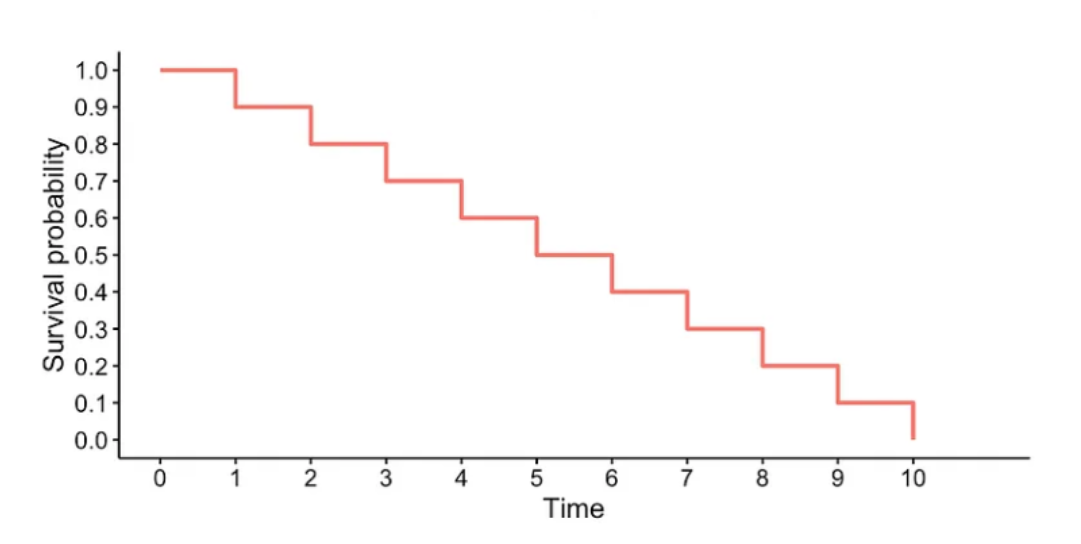
Generally you’ll observe that as the customer’s tenure increases, their survival prospects decrease. There also might be various bumps and dips around your standard product lifecycle (e.g 24 months if your a telco selling device contracts).
Calculating CLV
With the survival curve fitted we know the probability of a customer being alive at each of our desired time interval (on average).
We can then use the customers current service pricing per interval and multiply out by these probabilities to get a time interval revenue per customer dampened by the customer’s likelihood to live.
Use cases
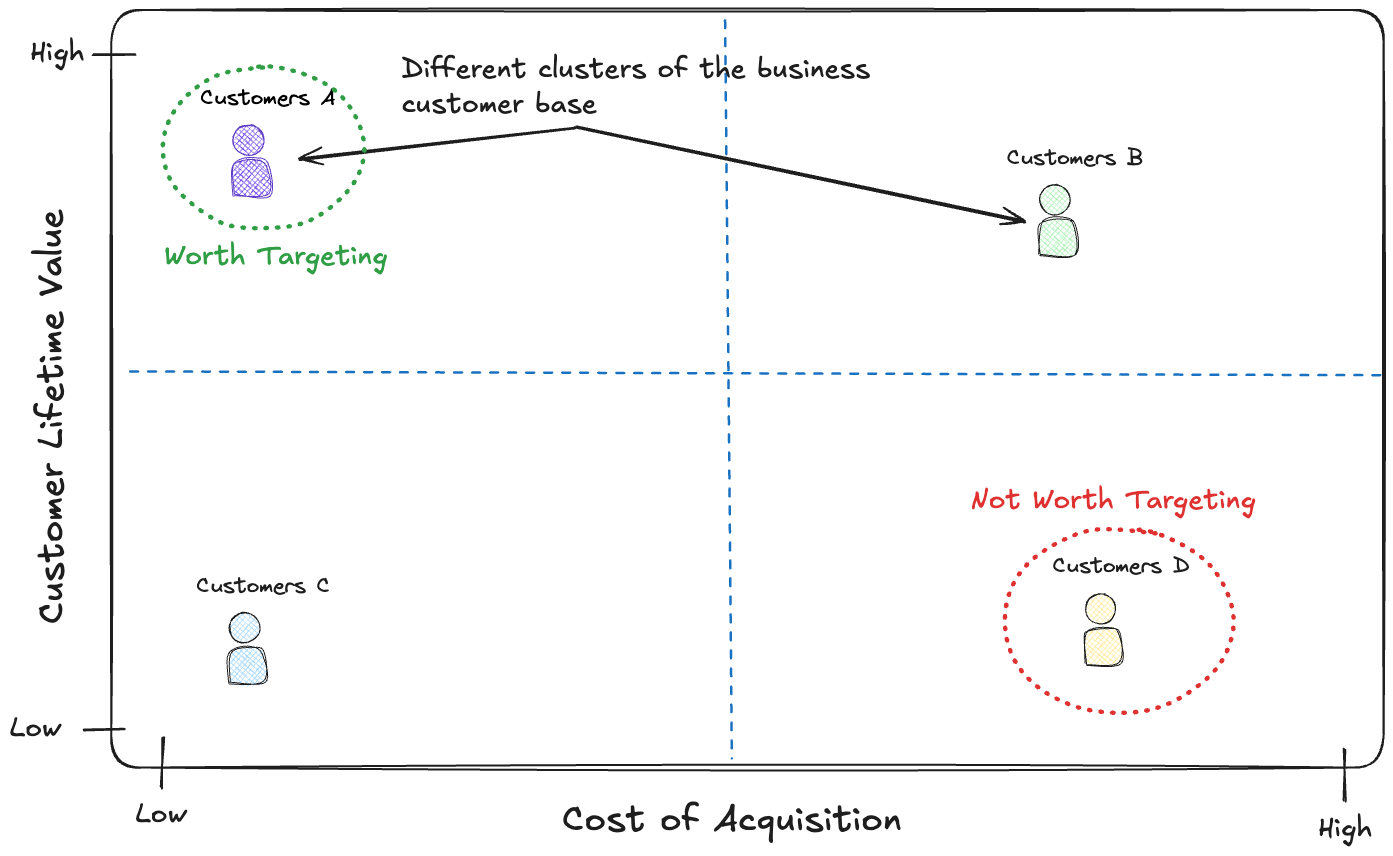
If you know the CLV for a customer then it can help with audience targeting especially if we know the Cost of Acuisition (CAC) for different audiences by creating a SWOT style chart (as shown below).
The group of customers A are low CAC and have high LTV so they should be prioritied for targeting as they are “low hanging fruit”. On the other hand group D are low CAC and have high LTV so they should be avoided.
Conclusion
CLV modelling is highly useful and provides critical insights that can help priortise and personalise experiences for those customers that are worth more. This can directly lead to more value generation for a business.
Resources
- Intro to survival analysis; lifelines package
- This package provides implementations of the Kaplan-Meier functionality that can be applied to your use case.
- Into to Kaplan-Meier functions
- This can help you undestand how these functions work.
